SciPyを使ってバネマスダンパ系のシミュレーションをやってみる

理論

scipy.integrate.odeintでは常微分方程式 \frac{d}{dt}\vec{u} =f\left( \vec{u} \right) を解くことができる。 バネマスダンパ系の運動方程式を \frac{d}{dt}\vec{u} =f\left( \vec{u} \right) の形に書き換えれば解を得られる。

バネマスダンパ系の運動方程式は次の通り。ここで Fは外力

\displaystyle ma = -cv - kx + F

ここで両辺をmで割る。

\displaystyle a ＝ -\frac{c}{m}v -\frac{k}{m}x + \frac{F}{m}

v= \frac{dx}{dt} であることを考慮すれば、現代制御でおなじみの方程式が導かれる

\displaystyle \frac{d}{dt} \begin{pmatrix} x \\v \\ \end{pmatrix} = \begin{pmatrix} 0 & 1\\ -c/m & -k/m \\ \end{pmatrix} \begin{pmatrix} x \\v \\ \end{pmatrix} + \begin{pmatrix} 0\\ -f/m\\ \end{pmatrix}

実装

from scipy.integrate import odeint
import matplotlib.pyplot as plt
import numpy as np

#外力
def exForce(u,t):
    return 0

#運動方程式
def equationOfMotion(u, t, m,c,k):
    f = exForce(u,t)
    A = np.array([
        [0,1],
        [-k/m, -c/m]])
    b = np.array([0,f/m])
    return np.dot(A, u) + b


if __name__ =="__main__":
    #バネマスダンパの係数
    m=1
    c=2
    k=5
    args= (m,c,k)
    
    #初期値
    x0 = 10
    v0 = 0
    u0=[x0,v0]
    
    #計算時間
    dt = 0.001
    stop = 10
    times=np.arange(0., stop+dt, dt)

    #解
    orient = odeint(equationOfMotion, u0, times, args)
    x=orient[:,0]
    v=orient[:,1]

    #グラフ表示
    plt.plot(times,x)
    plt.xlim(0,stop)
    plt.xlabel("t[s]")
    plt.ylabel("x[m]")
    plt.grid()
    plt.show()

出力結果

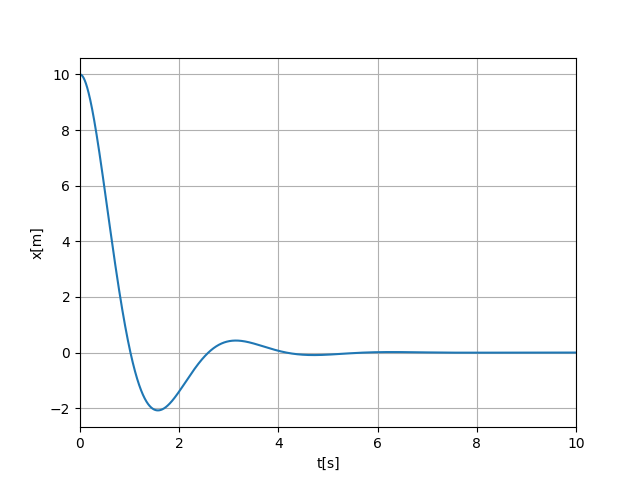
f:id:negizoku:20211120194827p:plain
mck

外力を変えてみる

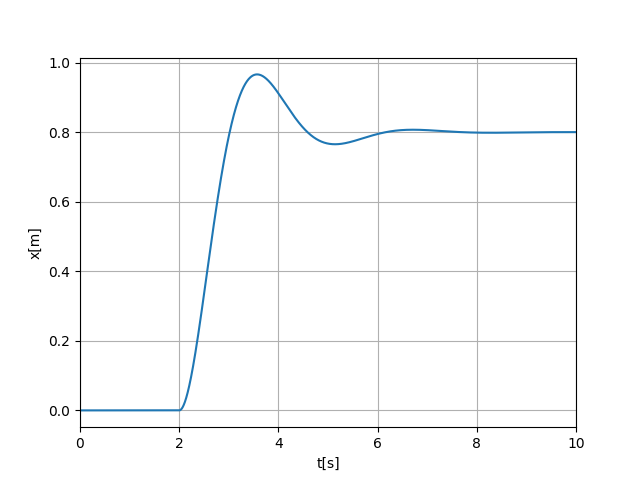
ステップ入力

def exForce(u,t):
    if(t>2):
        f=4
    else:
        f=0
    return f

f:id:negizoku:20211120195912p:plain
ステップ応答

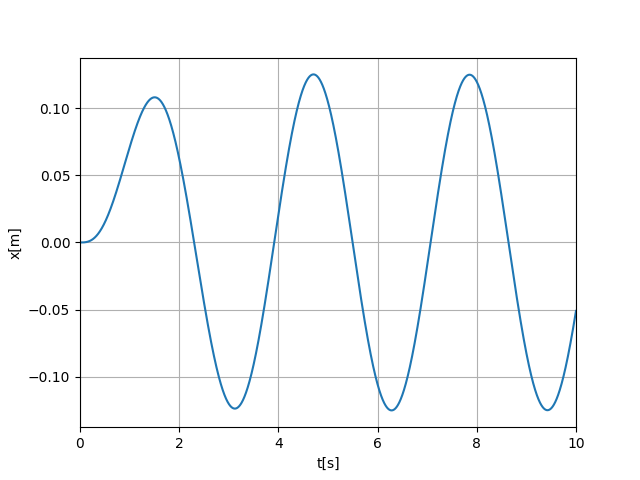
正弦波

from math import sin

#外力
def exForce(u,t):
    return 0.5*sin(2*t)

f:id:negizoku:20211120200504p:plain
正弦波応答